Содержание статьи
- Обработка чисел
- Двоичная система
- Перевод чисел из двоичной системы в десятичную и обратно
- Сложение
- Вычитание
- Умножение
- Арифметико-логические устройства
- Сумматор
- Универсальный сумматор-вычитатель
- Умножители
- Переходим к АЛУ
- Собираем АЛУ
- Однобитный полный сумматор
- Двухбитный сумматор
- Универсальный сумматор-вычитатель
- Выводы
Обработка чисел
Основная работа любого микропроцессора — это обработка чисел. А уже на ее основе совершаются другие, более сложные операции.
Цифровая электроника с самого начала
В своих прошлых статьях я рассказывал о двоичной системе счисления, алгебре логики и логических вентилях, электронных компонентах, микросхемах и многом другом интересном и полезном. Рекомендую ознакомиться, особенно если в этой статье встретятся непонятные вещи.
В основе работы компьютера лежит арифметико‑логическое устройство (АЛУ). Чтобы понять, как оно работает, давай разберем принцип, который позволяет компьютеру совершать операции. Но сначала я подробнее расскажу о самой двоичной системе.
Двоичная система
Думаю, ты уже имеешь некоторое представление о двоичном счислении. Все числа в двоичной системе состоят из двух цифр — нуля и единицы. Внутри компьютер использует ее для всех операций, даже если работает с десятичными или шестнадцатеричными числами.
Перевод чисел из двоичной системы в десятичную и обратно
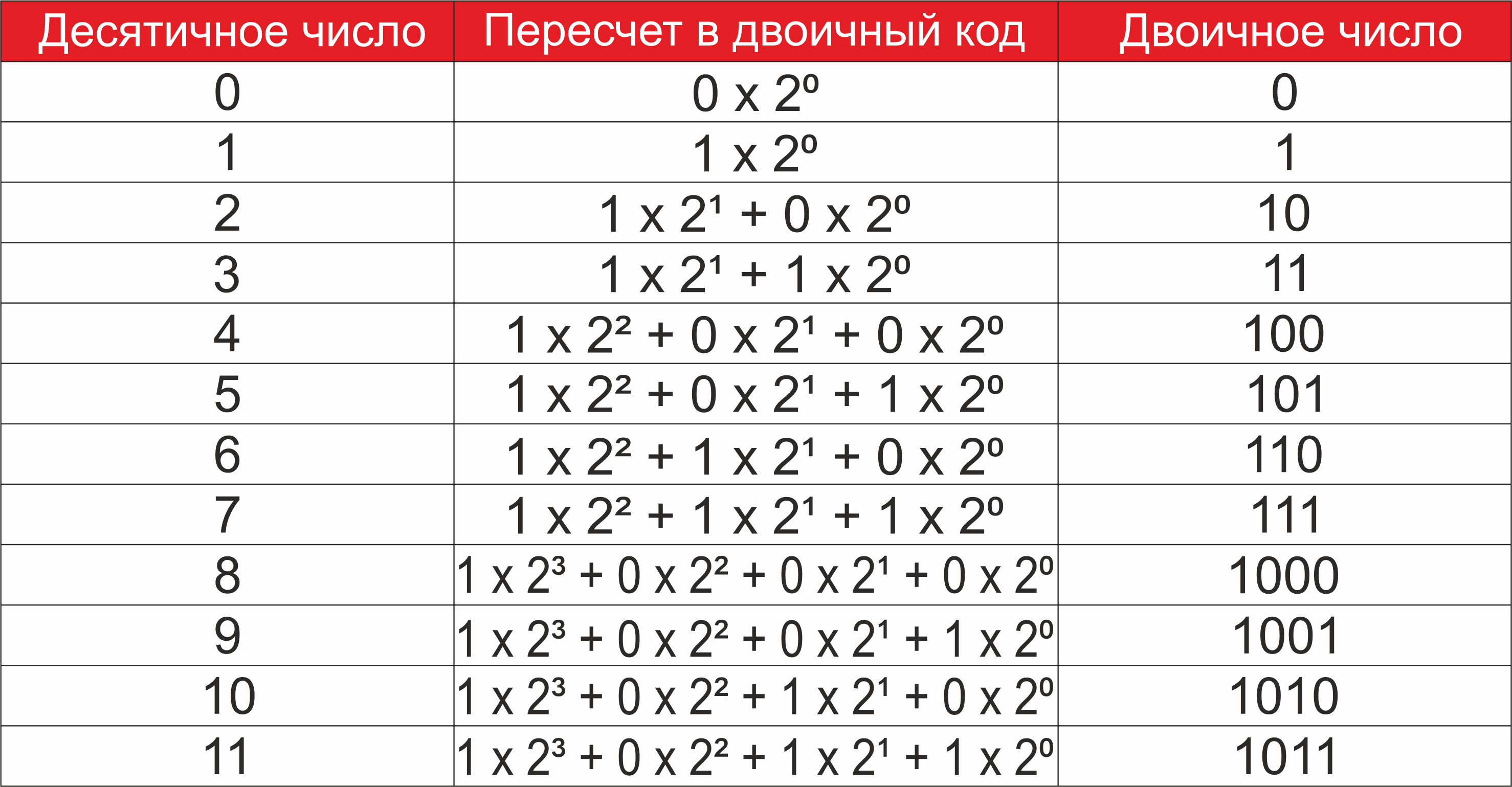
Переводить числа из одной системы в другую проще всего при помощи калькулятора, но для нас сейчас важно знать, как это делается, по шагам.
Число в десятичной системе счисления можно представить в виде суммы его цифр, помноженных на десять в степени разряда числа — от самого правого, которому соответствует 10 в нулевой степени, к самому левому, при том что степень каждый раз возрастает на единицу. Например:
389 = 3 ∙ 10² + 8 ∙ 10¹ + 9 · 10⁰ = 300 + 80 + 9
Точно так же можно раскладывать двоичные числа, только каждый разряд (самая правая цифра считается самым младшим разрядом) умножается не на степень десяти, а на степень двойки. В итоге мы получим число в десятичной системе. В качестве примера переведем число 1101 из двоичной в десятичную:
1101 = 1 ∙ 2³ + 1 · 2² + 0 · 2¹ + 1 · 2⁰ = 8 + 4 + 0 + 1 = 13
Чтобы перевести обратно, нужно использовать деление с остатком. Исходное число в десятичной системе делим на два, остаток от деления (1 или 0) записываем в первый разряд (самая правая цифра). Полученное частное снова делим на два и остаток записываем уже в следующий разряд. Так действуем, пока в результате деления не получится ноль. Пример ты можешь увидеть на картинке снизу.
Сложение
За операцию сложения в электронных чипах отвечает сумматор. Как складывать двоичные числа? Можно сложить в столбик точно так же, как десятичные. Поскольку цифр всего две, держать в уме и переносить здесь можно только единицу.
Всего возможных вариантов сложения цифр одного разряда четыре:
-
0+ 0 = 0 -
0+ 1 = 1 -
1+ 0 = 1 -
1+ 1 = 10
В последнем случае единица переходит в следующий разряд, результат записывается как «0 с переносом 1». Этот бит перенесенной единицы складывается с битом в следующем разряде.

Теперь рассмотрим более сложный пример со складыванием четырехбитных двоичных чисел. В этих случаях все единицы младшего значащего разряда дают в сумме бит нуля с переносом единицы в следующие разряды. Напоминаю, разряды считаются от меньшего к большему (справа налево). В следующем разряде мы снова получаем две единицы от переноса и единицы в разряде. Процесс повторяется до самого старшего значащего бита.
Аналогично и с другими числами в среднем примере. В последнем примере вышедший из младшего разряда бит переноса дает единицу и в сумму, и в бит переноса. Как видишь, это работает точно так же, как с десятичными числами, а может, даже и проще.
Вычитание
Если при сложении нам нужно переносить числа, то при вычитании потребуется занимать. Работает это точно так же, как при десятичном вычитании в столбик.
Продолжение доступно только участникам
Материалы из последних выпусков становятся доступны по отдельности только через два месяца после публикации. Чтобы продолжить чтение, необходимо стать участником сообщества «Xakep.ru».
Присоединяйся к сообществу «Xakep.ru»!
Членство в сообществе в течение указанного срока откроет тебе доступ ко ВСЕМ материалам «Хакера», позволит скачивать выпуски в PDF, отключит рекламу на сайте и увеличит личную накопительную скидку! Подробнее









